Page 38 - 2024-calc4e-SE proofs-4e.indd
P. 38
Sullivan 04 apcalc4e 45342 ch02 166 233 5pp August 7, 2023 12:54
188 Chapter 2 • The Derivative and Its Properties
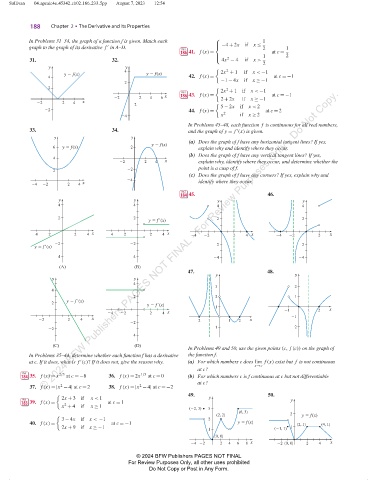
In Problems 31–34, the graph of a function f is given. Match each 1
−4 + 2x if x ≤
graph to the graph of its derivative f in A–D. PAGE 2 1
′
186 41. f (x) = at c =
2 1 2
31. 32. 4x − 4 if x >
2
y y
2
4 2x + 1 if x < −1
y f(x) y f(x)
4 42. f (x) = at c = −1
2 −1 − 4x if x ≥ −1
2 2
PAGE 2x + 1 if x < −1
2 2 4 6 x 186 43. f (x) = 2 + 2x if x ≥ −1 at c = −1
2 2 4 x
2 5 − 2x if x < 2
2 44. f (x) = at c = 2
4 x 2 if x ≥ 2
In Problems 45–48, each function f is continuous for all real numbers,
33. 34. and the graph of y = f (x) is given.
′
y y
(a) Does the graph of f have any horizontal tangent lines? If yes,
y f(x)
6 y f(x) 2 explain why and identify where they occur.
(b) Does the graph of f have any vertical tangent lines? If yes,
4
2 2 4 x explain why, identify where they occur, and determine whether the
2 point is a cusp of f.
2
(c) Does the graph of f have any corners? If yes, explain why and
4
x identify where they occur.
4 2 2 4
PAGE
184 45. 46.
y y y y
4 4 4 4
2 2 2 2
y 5 f 9(x)
4 x
4 x
4 x
x
24
24 © 2024 BFW Publishers PAGES NOT FINAL - For Review Purposes Only - Do Not Copy.
22
22
2
2
22
24
2
22
2
24
22 22 22 22
y 5 f 9(x)
24 24 24 24
(A) (B)
47. 48.
y y
y y
4
3 2
4
2 2 1
y 5 f 9(x)
2
y 5 f 9(x)
1 x
24 22 2 4 x 21 1 2
22 2 4 x 22 21 1 2 x 21
22
22 21 22
24
(C) (D)
In Problems 49 and 50, use the given points (c, f (c)) on the graph of
In Problems 35–44, determine whether each function f has a derivative the function f.
at c. If it does, what is f (c)? If it does not, give the reason why. (a) For which numbers c does lim f (x) exist but f is not continuous
′
x→c
at c?
PAGE 2/3 1/3
184 35. f (x) = x at c = −8 36. f (x) = 2x at c = 0 (b) For which numbers c is f continuous at c but not differentiable
at c?
2
2
37. f (x) = |x − 4| at c = 2 38. f (x) = |x − 4| at c = −2
49. 50.
2x + 3 if x < 1 y
PAGE y
183 39. f (x) = 2 at c = 1
x + 4 if x ≥ 1
( 2, 3) 3
(6, 3)
(2, 2) 2 y f(x)
3 − 4x if x < −1 2
40. f (x) = at c = −1 y f (x) (2, 1) (4, 1)
2x + 9 if x ≥ −1 ( 1, 1) 1
1
(0, 0)
4 2 2 4 6 8 x 2 (0, 0) 2 4 x
© 2024 BFW Publishers PAGES NOT FINAL
For Review Purposes Only, all other uses prohibited
Do Not Copy or Post in Any Form.