Page 45 - 2023-bfw-physics-stewart-3e-new.indd

Chapter Summary 327

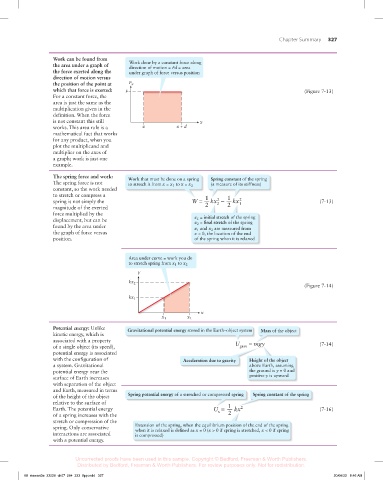
Work can be found from
the area under a graph of Work done by a constant force along
direction of motion = Fd = area
the force exerted along the under graph of force versus position
direction of motion versus
the position of the point at F x
which that force is exerted: F (Figure 7-13)
For a constant force, the
area is just the same as the
multiplication given in the
definition. When the force
is not constant this still x
works. This area rule is a x x + d
mathematical fact that works
for any product, when you
plot the multiplicand and
multiplier on the axes of
a graph; work is just one
example.
The spring force and work: Work that must be done on a spring Spring constant of the spring
The spring force is not
to stretch it from x = x 1 to x = x 2 (a measure of its stiffness)
constant, so the work needed
to stretch or compress a 1 1
2
spring is not simply the W = kx − kx 2 1 (7-13)
2
magnitude of the exerted 2 2
force multiplied by the
1
displacement, but can be x = initial stretch of the spring
x = nal stretch of the spring
2
found by the area under x and x are measured from
1
2
the graph of force versus x = 0, the location of the end
position. of the spring when it is relaxed
Area under curve = work you do
to stretch spring from x 1 to x 2
F
kx 2
(Figure 7-14)
kx 1

x
x 1 x 2
Potential energy: Unlike Gravitational potential energy stored in the Earth–object system Mass of the object
kinetic energy, which is
associated with a property
of a single object (its speed), U grav = mgy (7-14)
potential energy is associated
with the configuration of Acceleration due to gravity Height of the object
a system. Gravitational above Earth, assuming
potential energy near the the ground is y = 0 and
surface of Earth increases positive y is upward
with separation of the object
and Earth, measured in terms
of the height of the object Spring potential energy of a stretched or compressed spring Spring constant of the spring
relative to the surface of
Earth. The potential energy U = 1 kx 2 (7-16)
s
of a spring increases with the 2
stretch or compression of the
spring. Only conservative Extension of the spring, when the equilibrium position of the end of the spring
when it is relaxed is de ned as x = 0 (x > 0 if spring is stretched, x < 0 if spring
interactions are associated is compressed)
with a potential energy.

Uncorrected proofs have been used in this sample. Copyright © Bedford, Freeman & Worth Publishers.
Distributed by Bedford, Freeman & Worth Publishers. For review purposes only. Not for redistribution.

08_stewart3e_33228_ch07_284_333_8pp.indd 327 20/08/22 8:46 AM