Page 36 - 2022-bfw-morris-1e

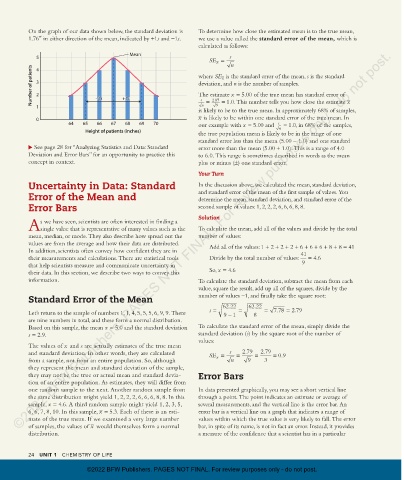
On the graph of our data shown below, the standard deviation is To determine how close the estimated mean is to the true mean,
1.76″ in either direction of the mean, indicated by +1s and -1s. we use a value called the standard error of the mean, which is
calculated as follows:
©2022 BFW Publishers. PAGES NOT FINAL. For review purposes only - do not post.
Mean s
5
SE x = n
Number of patients 3 2 where SE is the standard error of the mean, s is the standard
4
x
deviation, and n is the number of samples.
The estimate = 5.00 of the true mean has standard error of
x
–1s
+1
9
1 –1s +1s s s n = 2.87 = 1.0. This number tells you how close the estimate x
is likely to be to the true mean. In approximately 68% of samples,
0 x is likely to be within one standard error of the true mean. In
64 65 66 67 68 69 70 our example with = 5.00 and s = 1.0, in 68% of the samples,
x
Height of patients (inches) n
the true population mean is likely to be in the range of one
standard error less than the mean (5.00 - 1.0) and one standard
See page 28 for “Analyzing Statistics and Data: Standard error more than the mean (5.00 + 1.0). This is a range of 4.0
Deviation and Error Bars” for an opportunity to practice this to 6.0. This range is sometimes described in words as the mean
concept in context. plus or minus (±) one standard error.
Your Turn
Uncertainty in Data: Standard In the discussion above, we calculated the mean, standard deviation,
Error of the Mean and and standard error of the mean of the first sample of values. You
determine the mean, standard deviation, and standard error of the
Error Bars second sample of values: 1, 2, 2, 2, 6, 6, 6, 8, 8.

Solution
s we have seen, scientists are often interested in finding a
Asingle value that is representative of many values such as the To calculate the mean, add all of the values and divide by the total
mean, median, or mode. They also describe how spread out the number of values:
values are from the average and how their data are distributed. Add all of the values: 1 + 2 + 2 + 2 + 6 + 6 + 6 + 8 + 8 = 41
In addition, scientists often convey how confident they are in 41
their measurements and calculations. There are statistical tools Divide by the total number of values: = 4.6
that help scientists measure and communicate uncertainty in 9
x
their data. In this section, we describe two ways to convey this So, = 4.6
information. To calculate the standard deviation, subtract the mean from each
value, square the result, add up all of the squares, divide by the
Standard Error of the Mean number of values -1, and finally take the square root:
62.22 62.22
Let’s return to the sample of numbers 1, 1, 4, 5, 5, 5, 6, 9, 9. There s = 9 − 1 = 8 = 7.78 = 2.79
are nine numbers in total, and these form a normal distribution.
x
Based on this sample, the mean = 5.0 and the standard deviation To calculate the standard error of the mean, simply divide the
s = 2.9. standard deviation (s) by the square root of the number of
values:
The values of x and s are actually estimates of the true mean
and standard deviation. In other words, they are calculated SE = s = 2.79 = 2.79 = 0.9
from a sample, not from an entire population. So, although x n 9 3
they represent the mean and standard deviation of the sample,
they may not be the true or actual mean and standard devia- Error Bars
tion of an entire population. As estimates, they will differ from
one random sample to the next. Another random sample from In data presented graphically, you may see a short vertical line
the same distribution might yield 1, 2, 2, 2, 6, 6, 6, 8, 8. In this through a point. The point indicates an estimate or average of
sample, = 4.6. A third random sample might yield 1, 2, 3, 5, several measurements, and the vertical line is the error bar. An
x
6, 6, 7, 8, 10. In this sample, = 5.3. Each of these is an esti- error bar is a vertical line on a graph that indicates a range of
x
mate of the true mean. If we examined a very large number values within which the true value is very likely to fall. The error
of samples, the values of x would themselves form a normal bar, in spite of its name, is not in fact an error. Instead, it provides
distribution. a measure of the confidence that a scientist has in a particular

24 UNIT 1 CHEMISTRY OF LIFE

©2022 BFW Publishers. PAGES NOT FINAL. For review purposes only - do not post.

03_morrisapbiology1e_11331_Unit1_Tut1_20-25_3pp.indd 24 10/04/21 9:13 AM